基础

解题步骤

  1. 确定dp数组（dp table）以及下标的含义

  2. 确定递推公式

  3. dp数组如何初始化

  4. 确定遍历顺序

    举例推导dp数组

当遇到bug时，可以通过打印dp数组看看是不是和自己预先推导的一样

如果打印出来的dp数组和自己预先推导的一样，那么就是自己的递归公式、初始化或者遍历顺序出现问题

如果和自己预先模拟推导的不一样，那么就是代码实现细节有问题


题目

509. 斐波那契数

1
2
3
4
5
6
7
8
9
10
11
12
class Solution {
    public int fib(int n) {
        if (n < 2) return n;
        int[] dp = new int[n + 1];
        dp[0] = 0;
        dp[1] = 1;
        for (int i = 2; i <= n; i++) {
            dp[i] = dp[i - 1] + dp[i - 2];
        }
        return dp[n];
    }
}

精简代码之后

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution {
    public int fib(int n) {
        if(n<2) return n;
        int sum = 0;
        int num1 = 0;
        int num2 = 1;
        for(int i = 2;i<=n;i++){
            sum = num1+num2;
            num1 = num2;
            num2 = sum;
        }
        return sum;
    }
}

70. 爬楼梯

image-20221115170807779

dp[1]代表的是一层阶梯的情况

dp[2]代表的是两层阶梯的情况

所以求n层阶梯有几种情况，即求dp[n]即可

image-20221115165028740

通过观察可以得出，dp[n]=dp[n-1]+dp[n-2]（递推公式）

关于dp数组的初始化，此处不讨论dp[0]的初始化，使用dp[1]代表一层阶梯，依次类推

1
2
3
4
5
6
7
8
9
10
11
12
class Solution {
        public int climbStairs(int n) {
            if (n <= 2) return n;
            int[] dp = new int[n + 1];
            dp[1] = 1;
            dp[2] = 2;
            for (int i = 3; i <= n; i++) {
                dp[i] = dp[i - 1] + dp[i - 2];
            }
            return dp[n];
        }
    }

使用变量记录代替数组

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
        public int climbStairs(int n) {
            if (n <= 2) return n;
            int sum = 0;
            int num1 = 1;
            int num2 = 2;
            for (int i = 3; i <= n; i++) {
                //代表前两个数相加，f(i - 1) + f(i - 2)
                sum = num1+num2;
                //记录f(i - 1)，即下一轮的f(i - 2)
                num1 = num2;
                //记录f(i - 2)，即下一轮的f(i - 1)
                num2 = sum;
            }
            return sum;
        }
    }

746. 使用最小花费爬楼梯

image-20221115200508139

  • cost数组：楼梯第 i 个台阶向上爬需要支付的费用

  • dp数组：到达第 i 台阶所花费的最少体力为dp[i]

跳到dp[i]所需要的费用是，dp[i - 1] + cost[i - 1] 或者是 dp[i - 2] + cost[i - 2]（此处花费是上一个台阶的花费加上之前的所有台阶的花费，比如1->3->5->7，5跳到7的总花费是5->7的花费加上之前1->3->5的所有花费）

因为要求支付的最小费用，所以得出递推公式为：dp[i] = Math.min(dp[i - 1] + cost[i - 1], dp[i - 2] + cost[i - 2])

初始化dp数组，题目的要求为，“可以选择从下标为 0 或下标为 1 的台阶开始爬楼梯”，所以到达第 0 个台阶是不需要花费的，所以可以将dp[0]与dp[1]都初始化为0

1
2
3
4
5
6
7
8
9
10
11
class Solution {
    public int minCostClimbingStairs(int[] cost) {
        int[] dp = new int[cost.length + 1];
        dp[0] = 0;
        dp[1] = 0;
        for (int i = 2; i <= cost.length; i++) {
            dp[i] = Math.min(dp[i-1]+cost[i-1],dp[i-2]+cost[i-2] );
        }
        return dp[cost.length];
    }
}

使用变量记录代替数组

1
2
3
4
5
6
7
8
9
10
11
12
13
class Solution {
    public int minCostClimbingStairs(int[] cost) {
        int dp1 = 0;
        int dp2 = 0;
        for (int i = 2; i <= cost.length; i++) {
            int dpTemp = Math.min(dp1+cost[i-2],dp2+cost[i-1]);
            //记录前两位元素
            dp1 = dp2;
            dp2 = dpTemp;
        }
        return dp2;
    }
}

62. 不同路径

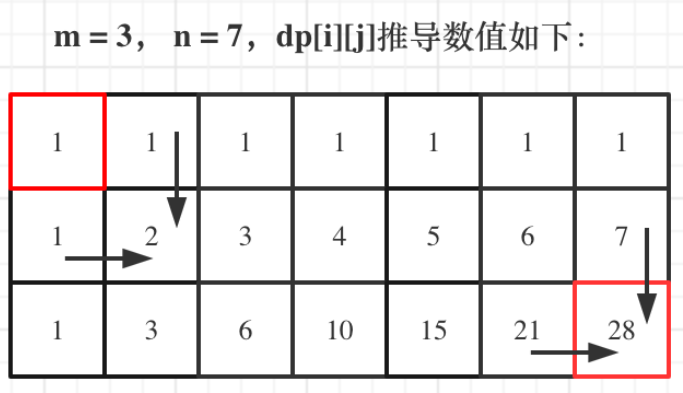
image-20221116225356425

  • dp数组的定义为：dp[i][j] ：表示从(0,0)出发，到(i, j) 有dp[i][j]条不同的路径

  • 通过图可以发现，当我们对 dp[i][j] 进行求解的时候，是通过它上方和左方的点进行推断的，上方的点向下走一步就到达 dp[i][j] ，左方的点也同样如此。上方和左方的点分别代表到达该点的路径条数，所以dp[i][j] 就可以表示为上方和左方结点路径条数之和，即递推公式：dp[i][j] = dp[i-1][j] + dp[i][j-1]

  • 初始化：因为dp[i][j]都是通过上方和左方的点推算出来的，所以最上面一行和最左边的一列必须进行初始化，由题目可以得知，到达最上面一行和最左边的一列都只有一种走法，所以dp[0][j] 和 dp[i][0] 都应该初始化为1

  • 确定遍历顺序：因为所有点都是通过上方和下方进行推导的，所以遍历的时候也应该从上到下，从左到右进行遍历

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
    public int uniquePaths(int m, int n) {
        int[][] dp = new int[m][n];
        //初始化dp数组
        for (int i = 0; i < m; i++) {
            dp[i][0] = 1;
        }
        for (int i = 0; i < n; i++) {
            dp[0][i] = 1;
        }
        //遍历
        for (int i = 1; i < m; i++) {
            for (int j = 1; j < n; j++) {
                dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
            }
        }
        return dp[m - 1][n - 1];
    }
}

63. 不同路径 II

image-20221118140750260 image-20221118140813141

对于路径中有障碍的情况，我们将该点的dp数组标识为0，递推公式对比上一种情况有所改变

1
2
3
4
// 当(i, j)没有障碍的时
if (obstacleGrid[i][j] == 0) { 
    dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
}

dp数组的初始化：因为dp[i][j]都是通过上方和左方的结点进行推断的，所以必须对上层和左层的结点进行初始化，将障碍在上层和左层出现时，都应该将障碍右边或下边的结点赋值为0。（因为该结点无法到达）

image-20221118142225274

遍历顺序：因为都是从上层推断到下层，左层推断到右层，所以遍历顺序为从上到下，从左到右

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
public int uniquePathsWithObstacles(int[][] obstacleGrid) {
    int m = obstacleGrid.length;
    int n = obstacleGrid[0].length;
    int[][] dp = new int[m][n];
    //起点或终点出现了障碍,直接返回0条路径
    if (obstacleGrid[m - 1][n - 1] == 1 || obstacleGrid[0][0] == 1) {
        return 0;
    }
    //初始化上层和左层的路径
    for (int i = 0; i < m && obstacleGrid[i][0] == 0; i++) {
        dp[i][0] = 1;
    }
    for (int j = 0; j < n && obstacleGrid[0][j] == 0; j++) {
        dp[0][j] = 1;
    }
    //遍历
    for (int i = 1; i < m; i++) {
        for (int j = 1; j < n; j++) {
            if (obstacleGrid[i][j] == 0){
                dp[i][j] = dp[i-1][j] + dp[i][j-1];
            }
        }
    }
    return dp[m-1][n-1];
}

343. 整数拆分

image-20221122211501597

dp数组的定义：dp[i]表示分拆数字 i 时，可以得到的最大乘积

递推公式：dp[i]最大乘积可以通过从1遍历 j，然后 j * (i - j) 得出dp[i]最大乘积，一种是j * dp[i - j]（这种相当于拆分i-j）所以，比较(i - j) * j和dp[i - j] * j取最大的即可。dp[i] = Math.max(dp[i], max((i - j) * j, dp[i - j] * j));

j * (i - j)是单纯的把整数 i 拆分为两个数 也就是 i 和 i - j，再相乘
j * dp[i - j]是将 i 拆分成两个以及两个以上的个数，再相乘

注意：因为 j 是从1开始遍历，拆分 j 的情况，在遍历 j 的过程中其实都计算了

dp数组的初始化：因为拆分0和拆分1时，讨论最大乘积是没有意义的，所以此处只初始化dp[2] = 1

image-20221122212526519 
1
2
3
4
5
6
7
8
9
10
11
12
13
class Solution {
    public int integerBreak(int n) {
        int[] dp = new int[n + 1];
        dp[2] = 1;
        for (int i = 3; i <= n; i++) {
            for (int j = 1; j <= i - j; j++) {
                // 此处 j 最大值为 i-j，更大则重复了，没有意义
                dp[i] = Math.max(dp[i], Math.max(j * (i - j), j * dp[i - j]));
            }
        }
        return dp[n];
    }
}

96. 不同的二叉搜索树

image-20221123102437044 image-20221123102737602

dp数组的定义：dp[i] 表示1到i为节点组成的二叉搜索树的个数为dp[i]

以dp[3]为例，dp[3] = 元素 1 为头结点搜索树的数量 + 元素 2 为头结点搜索树的数量 + 元素 3 为头结点搜索数的数量

  • 元素1为头结点搜索树的数量 = 右子树有2个元素的搜索树数量 + 左子树有0个元素的搜索树数量
  • 元素2为头结点搜索树的数量 = 右子树有1个元素的搜索树数量 + 左子树有1个元素的搜索树数量
  • 元素3为头结点搜索树的数量 = 右子树有0个元素的搜索树数量 + 左子树有2个元素的搜索树数量

有2个元素的搜索树数量就是dp[2]，有1个元素就是dp[1]，有0个元素就是dp[0]

所以dp[3] = dp[2]*dp[0] + dp[1]*dp[1] + dp[0]*dp[2]

image-20221123103632145

递推公式：dp[i] += dp[以 j 为头结点左子树节点数量] * dp[以 j 为头结点右子树节点数量]

即为dp[i] += dp[j - 1] * dp[i - j] ，j-1 为 j 为头结点左子树节点数量，i-j 为以 j 为头结点右子树节点数量

初始化：最开始时，看成一颗空的二叉搜索树，初始化dp[0] = 1，dp[1] = 1，避免了在后面相乘时，与0相乘则乘法的结果就都变成0

1
2
3
4
5
6
7
8
9
10
11
12
class Solution {
    public int numTrees(int n) {
        int[] dp = new int[n + 1];
        dp[0] = 1;dp[1] = 1;
        for (int i = 2; i <= n; i++) {
            for (int j = 1; j <= i; j++) {
                dp[i] += dp[j - 1] * dp[i - j];
            }
        }
        return dp[n];
    }
}
1