概述

一般可以用回溯法解决以下问题

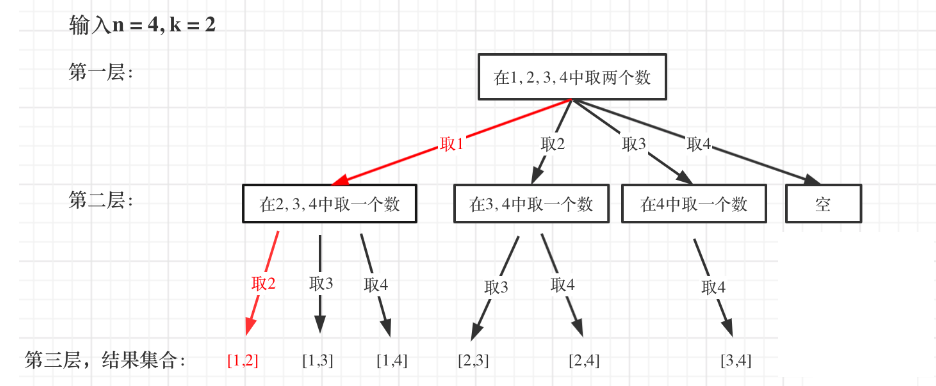
组合问题：N个数⾥⾯按⼀定规则找出k个数的集合
切割问题：⼀个字符串按⼀定规则有几种切割⽅式
子集问题：⼀个N个数的集合⾥有多少符合条件的子集
排列问题：N个数按⼀定规则全排列，有几种排列方式
棋盘问题：N皇后，解数独

回溯法的问题都可以抽象看为树形结构

for循环可以理解是横向遍历，递归看成纵向遍历，这样就把这棵树全遍历完了，一般来说，搜索叶子节点就是找的其中一个结果

void backtracking(参数) {
    if (终止条件) {
        存放结果;
        return;
    }

    for (选择：本层集合中元素（树中节点孩子的数量就是集合的大小）) {
        处理节点;
        backtracking(路径，选择列表); // 递归
        回溯，撤销处理结果
    }
}

组合问题

77.组合

class Solution {
    //存储最后的结果
    List<List<Integer>> res = new ArrayList<>();
    //存储一个组合
    LinkedList<Integer> temp = new LinkedList<>();

    public List<List<Integer>> combine(int n, int k) {
        backtracking(n, k, 1);
        return res;
    }

    private void backtracking(int n, int k, int start) {
        //终止条件 (递归到树形结构的叶子节点)
        if (temp.size() == k) {
            res.add(new ArrayList<>(temp));
            return;
        }
        for (int i = start; i <= n; i++) {
            temp.add(i);
            backtracking(n, k, i + 1);
            //回溯，撤销已经被处理的结点
            temp.removeLast();
        }
    }
}

对该代码进行剪枝优化

当n，k都等于4时（则返回1~4中所有4个数的组合）此时只需要进行一次遍历就可以获得结果，其他的遍历都是没有意义的

所以可以在递归的每一层for循环里选择起始位置，将代码进行修改

1
2
3

for (int i = startIndex; i <= n; i++)
//改为
for (int i = startIndex; i <= n - (k - temp.size()) + 1; i++)

temp.size()：代表的是，已经选择的元素个数
k - temp.size()：代表的是，还需要的元素个数
n - (k - temp.size()) + 1：代表的是，在集合n中至多要从该起始位置进行遍历

216. 组合总和 III

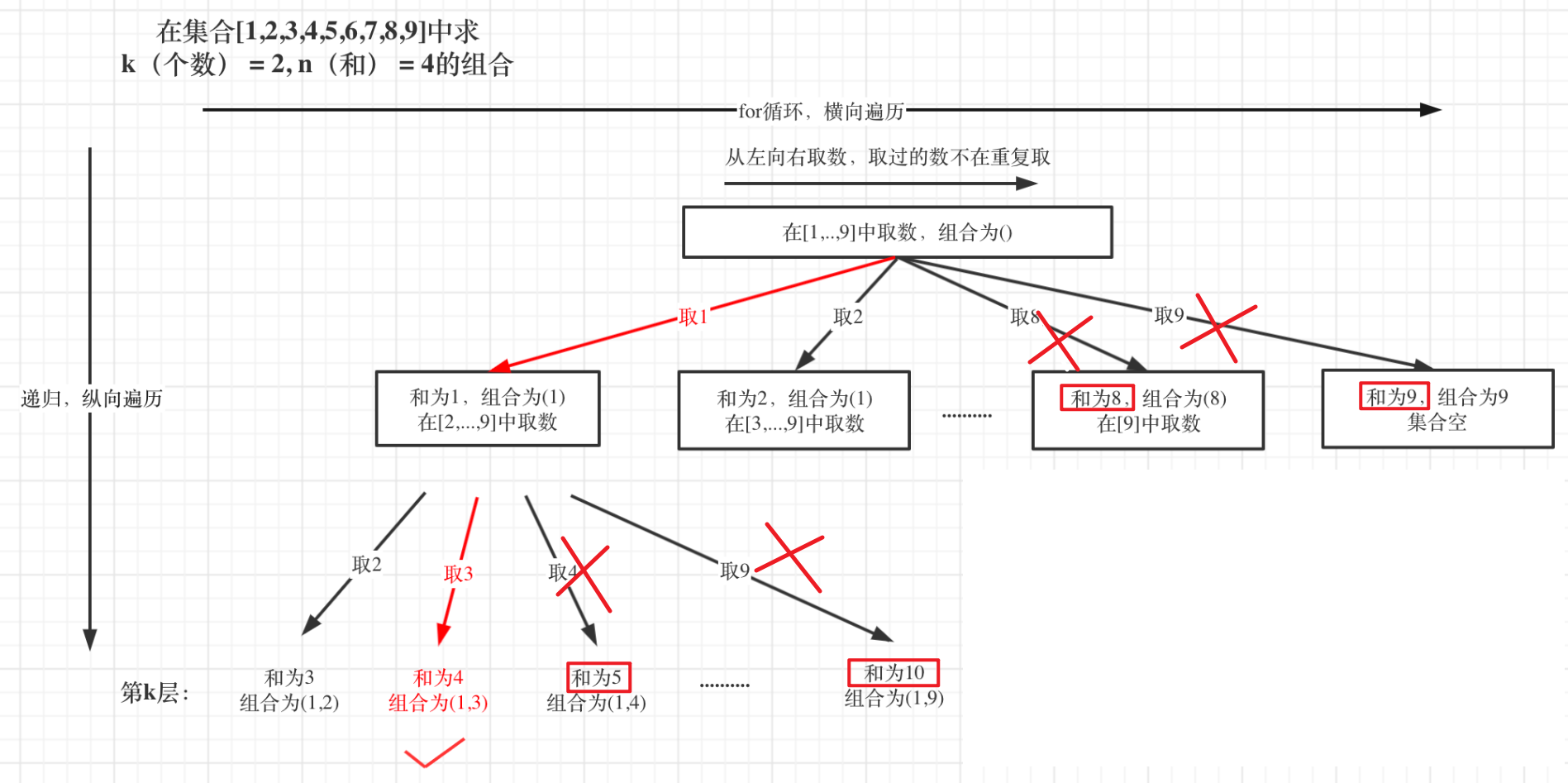
暴力回溯

该题与上一题类似，只不过现在需要在[1…9]集合中查找数，k就相当于树的深度

所以终止条件就是收集到的元素的个数与k相等，当终止时，则说明该组合符合要求，需要收集该组合

class Solution {
    List<List<Integer>> res = new ArrayList<>();
    LinkedList<Integer> temp = new LinkedList<>();

    public List<List<Integer>> combinationSum3(int k, int n) {
        backtracking(n, 0, 1, k);
        return res;
    }

    private void backtracking(int target, int sum, int start, int k) {
        if (temp.size() == k) {
            if (sum == target) {
                res.add(new ArrayList<>(temp));
                return;
            }
        }
        for (int i = start; i <= 9; i++) {
            temp.add(i);
            sum += i;
            backtracking(target, sum, i + 1, k);
            //回溯
            temp.removeLast();
            sum -= i;
        }
    }
}

剪枝优化

通过题目可以发现当选取元素之和已经超过目标值时，后面的组合遍历就没有意义了，同时for循环的范围和上一题类似，也可以进行剪枝，具体代码如下：

//在递归函数中加上该条件的判断
if (sum > target) {
    return;
}

1
2
3

for(int i = start; i <= 9; i++)
//优化为
for (int i = start; i <= 9 - (k - temp.size()) + 1; i++)

39. 组合总和

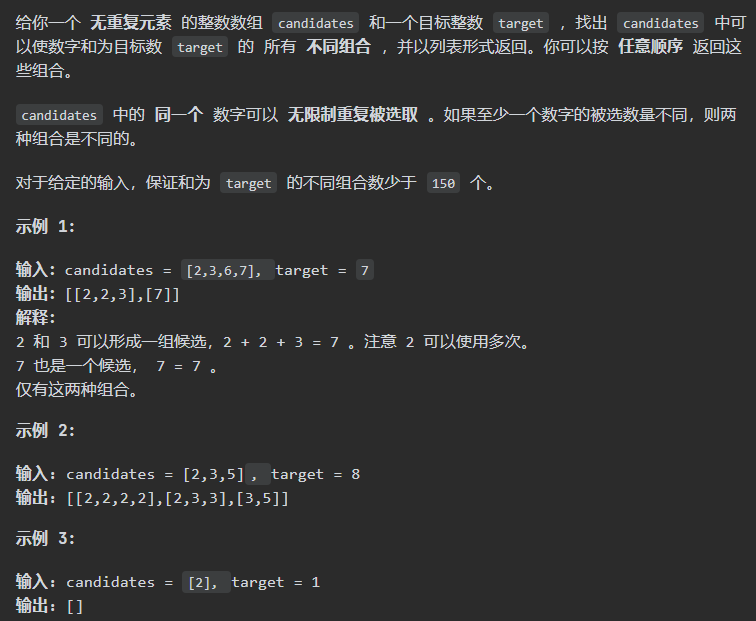
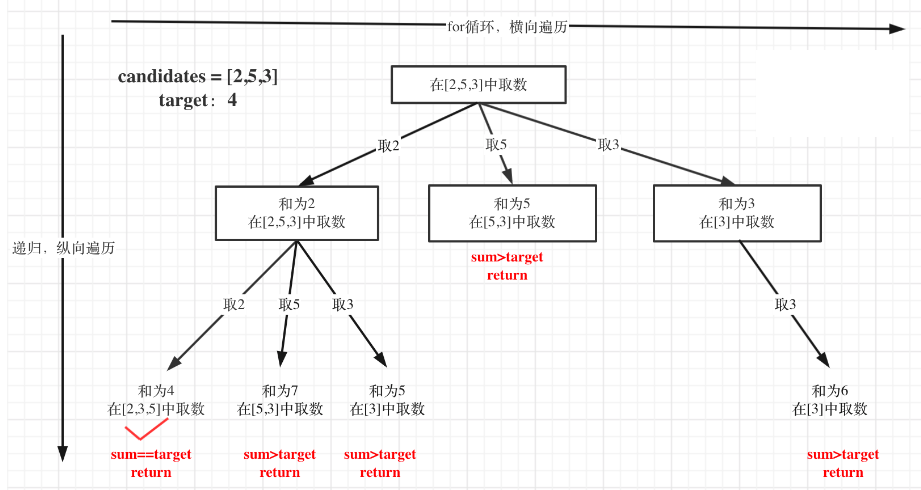
暴力回溯

递归的终止只有两种情况，sum大于target和sum等于target

sum等于target的时候，需要收集结果

注意：进行重复选取

class Solution{
        public List<List<Integer>> combinationSum(int[] candidates, int target) {
            //用来存储最终结果
            List<List<Integer>> res = new ArrayList<>();
            //用来存储一个组合
            Deque<Integer> temp = new ArrayDeque<>();
            backtracking(res, temp,candidates,target,0,0);
            return res;
        }

        /**
         * @param start 定义了每层递归的起始位置
         */
        private void backtracking(List<List<Integer>> res, Deque<Integer> temp, int[] candidates, int target, int sum, int start) {
            int length = candidates.length;
            //target 为负数和 0 的时候不再继续向下递归
            if (sum > target) {
                return;
            }
            if (sum == target) {
                res.add(new ArrayList<>(temp));
                return;
            }
            for (int i = start; i < length; i++) {
                //将符合要求的数字加入到组合中
                sum += candidates[i];
                temp.add(candidates[i]);
                /**
                 * 递归，进行下一层数字的选取
                 * 此处为i，而不是i+1是为了保证
                 * 当前元素选取后，下一层仍然有当前元素，以实现重复选取
                 */
                backtracking(res, temp, candidates, target, sum, i);
                //回溯
                sum -= candidates[i];
                temp.removeLast();
            }
        }
    }

剪枝优化

也可以将上题中创建分支时做减法，改成创建分支时做加法，更方便理解

此时递归结束的判断依据为：sum大于target

但是对于sum已经大于target的情况，其实是依然进入了下一层递归，只是下一层递归结束判断的时候，会判断sum > target的话就返回，其实如果已经知道下一层的sum会大于target，就没有必要进入下一层递归了

所以，可以对本来的 candidates[] 数组进行排序，排序后，在递归前进行判断，如果下一层的sum（sum + candidates[i]）已经大于target，就直接结束for循环遍历

class Solution {
        public List<List<Integer>> combinationSum(int[] candidates, int target) {
            //用来存储最终结果
            List<List<Integer>> res = new ArrayList<>();
            //用来存储一个组合
            List<Integer> temp = new ArrayList<>();
            //对原本数组进行排序
            Arrays.sort(candidates);
            backtracking(res, temp,candidates,target,0,0);
            return res;
        }

        /**
         * @param start 定义了每层递归的起始位置
         */
        private void backtracking(List<List<Integer>> res, List<Integer> temp, int[] candidates, int target, int sum, int start) {
            int length = candidates.length;
            //当找到了数字之和为target时，即该组合为结果，加入到res中
            if (sum == target){
                res.add(new ArrayList<>(temp));
                return;
            }
            for (int i = start; i < length; i++) {
                //如果新添加的数字大于target，说明不应该加入该数字，终止遍历
                if (sum + candidates[i] > target){
                    break;
                }
                //将符合要求的数字加入到组合中
                temp.add(candidates[i]);
                /**
                 * 递归，进行下一层数字的选取
                 * 此处为i，而不是i+1是为了保证
                 * 当前元素选取后，下一层仍然有当前元素，以实现重复选取
                 */
                backtracking(res, temp, candidates, target, sum + candidates[i], i);
                //回溯，移除temp数组中的最后一个元素
                temp.remove(temp.size()-1);
            }
        }
    }

17. 电话号码的字母组合

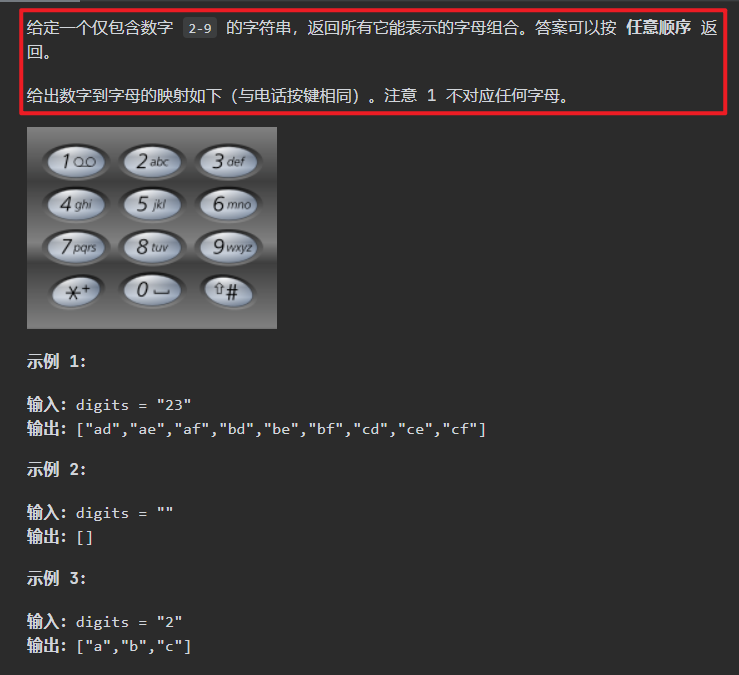
树的深度是由输入的数字的个数来决定

树的宽度是由每一个数字对应的字母长度来控制

终止条件为当前递归到数字的位置等于输入的数字个数

class Solution {
    List res = new ArrayList<>();
    //因为使用大量拼接，所以使用StringBuilder来进行存储
    StringBuilder temp = new StringBuilder();
    
    public List<String> letterCombinations(String digits) {
        if (digits.length() == 0) {
            return res;
        }
        String[] numMapping = new String[]{
                "",     // 0
                "",     // 1
                "abc",  // 2
                "def",  // 3
                "ghi",  // 4
                "jkl",  // 5
                "mno",  // 6
                "pqrs", // 7
                "tuv",  // 8
                "wxyz"  // 9
        };
        backtracking(digits, numMapping, 0);
        return res;
    }

    /**
     * @param startNum 表示当前递归到数字的位置
     */
    private void backtracking(String digits, String[] numMapping, int startNum) {
        //当遍历到末尾时，搜索过程结束，收获结果
        if (startNum == digits.length()) {
            res.add(temp.toString());
            return;
        }
        //取出digits中的数据，str表示数字所映射的字符串
        String str = numMapping[digits.charAt(startNum) - '0'];
        for (int i = 0; i < str.length(); i++) {
            temp.append(str.charAt(i));
            //递归
            backtracking(digits, numMapping, startNum + 1);
            //回溯
            temp.deleteCharAt(temp.length() - 1);
        }
    }
}

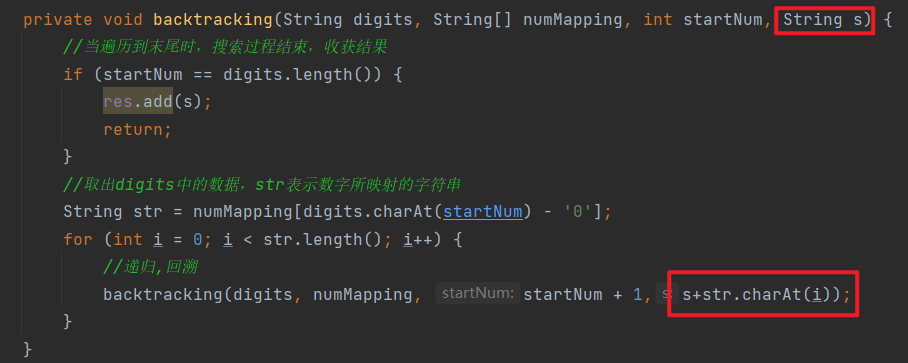
将回溯隐藏在递归中

在上述解法中，可以发现，需要取出字符串中的每一个字符，并将他们拼接成字符串，回溯时再将该字符删除掉，回到原本的状态

所以该字符串temp其实没变化过，可以在递归函数中，额外定义一个字符串s。当递归时，将s进行拼接，进行递归，而递归后，字符串s本身仍然不变，省去了再次回溯的过程

class Solution {
    List res = new ArrayList<>();
    public List<String> letterCombinations(String digits) {
        if (digits.length() == 0) {
            return res;
        }
        String[] numMapping = new String[]{
                "",     // 0
                "",     // 1
                "abc",  // 2
                "def",  // 3
                "ghi",  // 4
                "jkl",  // 5
                "mno",  // 6
                "pqrs", // 7
                "tuv",  // 8
                "wxyz"  // 9
        };
        backtracking(digits, numMapping, 0, "");
        return res;
    }

    private void backtracking(String digits, String[] numMapping, int startNum, String s) {
        if (startNum == digits.length()) {
            res.add(s);		//注意此处的变化
            return;
        }
        //取出digits中的数据，str表示数字所映射的字符串
        String str = numMapping[digits.charAt(startNum) - '0'];
        for (int i = 0; i < str.length(); i++) {
            //递归,回溯（注意此处的变化）
            backtracking(digits, numMapping, startNum + 1,s+str.charAt(i));
        }
    }
}

40. 组合总和 II

递归终止条件为：sum > target 和 sum == target

注意：该题与39. 组合总和不同的是，candidates中的每个数字只能使用一次，而且candidates内包含有重复元素，结果不能包含重复的元素，所以该题目需要进行去重操作

使用数组进行去重

可以使用一个used数组来进行去重的判断，将选取后的数字所对应的used数组标记为true

注意：要去重的是同一树层上使用过的数字，而不是同一树枝上的重复元素，要去重的是出现的相同组合，而不是一个组合里面的相同元素

在同一树枝上的都是一个组合里的元素
在同一个树层上的为不同组合的元素

在for循环遍历中，如果candidates[i] == candidates[i - 1] && used[i - 1] == false

就说明：前一个树枝选取的元素和当前树枝选取的元素一样，当前已经重复选取了

注意：此处必须要添加used[i - 1] == true这个条件，如果不加上这个条件，则表示的是同一个树枝里的一个组合

因为在同一个树层中used[i - 1] == false才能表示当前取的candidates[i]是从candidates[i - 1]回溯而来的，而used[i - 1] == true，说明是进入下一层递归，去下一个数，所以是树枝上，我们不需要去重一个组合里面的相同元素。

class Solution {
    List<List<Integer>> res = new ArrayList<>();
    LinkedList<Integer> temp = new LinkedList<>();
    //标记数组
    boolean[] used;

    public List<List<Integer>> combinationSum2(int[] candidates, int target) {
        used = new boolean[candidates.length];
        //为了将重复的数字都放到一起，先进行排序
        Arrays.sort(candidates);
        backtracking(candidates, target, 0, 0);
        return res;
    }

    private void backtracking(int[] candidates, int target, int start, int sum) {
        if (sum == target) {
            res.add(new ArrayList<>(temp));
        }
        for (int i = start; i < candidates.length; i++) {
            if (sum + candidates[i] > target) {
                break;
            }
            //出现重复的结点，直接跳过
            if (i > 0 && candidates[i] == candidates[i - 1] && !used[i - 1]) {
                continue;
            }
            //将当前选取的结点进行标记
            used[i] = true;
            temp.add(candidates[i]);
            //每个结点只能选择一次，所以下次递归的时候，从下一位开始
            backtracking(candidates, target, i + 1, sum + candidates[i]);
            //回溯
            used[i] = false;
            temp.removeLast();
        }
    }
}

不使用数组进行去重

candidates[i] == candidates[i - 1]这个条件控制的仅仅是前后元素是否相同，如果单纯使用这个条件就会导致同一树枝出现的相同元素也会去重，不符合题目要求

加上了i > strat这个条件后，如果在同一个树枝就会发现，i==start这个条件是始终满足的，只有在同一个树层时才会出现i>start这种情况，所以该条件可以对同一个树层使用过的元素进行去重，而不会错误地将同一个树枝的元素进行去重

1
2
3

if (i > strat && candidates[i] == candidates[i - 1]) {
    continue;
}

完整代码如下：

class Solution {
    List<List<Integer>> res = new ArrayList<>();
    LinkedList<Integer> temp = new LinkedList<>();

    public List<List<Integer>> combinationSum2(int[] candidates, int target) {
        //为了将重复的数字都放到一起，先进行排序
        Arrays.sort(candidates);
        backtracking(candidates, target, 0, 0);
        return res;
    }

    private void backtracking(int[] candidates, int target, int start, int sum) {
        if (sum == target) {
            res.add(new ArrayList<>(temp));
        }
        for (int i = start; i < candidates.length; i++) {
            if (sum + candidates[i] > target) {
                break;
            }
            //出现重复的结点，直接跳过
            if (i > start && candidates[i] == candidates[i - 1]) {
                continue;
            }
            //将当前选取的结点进行标记
            temp.add(candidates[i]);
            //每个结点只能选择一次，所以下次递归的时候，从下一位开始
            backtracking(candidates, target, i + 1, sum + candidates[i]);
            //回溯
            temp.removeLast();
        }
    }
}

分割问题

131. 分割回文串

切割问题与组合问题类似，组合问题通过在数组里面获取数字，而切割问题则是在数组里面截取数字，所以需要定义一条分割线。分割线其实与组合问题一样，都表示下一轮递归的起始位置

终止条件为：起始位置已经大于字符串s的长度，此时说明找到了一组切割的方案，所以终止*
判断是否回文：采用双指针的方法对字符串进行检验
截取字符串：在循环for (int i = startIndex; i < s.size(); i++)中，在判断子串为回文后，可以通过String substring = s.substring(start, i + 1);进行切割

注意：切割过的位置不能重复切割，所以在递归的时候，使用backtracking(s, i + 1);

class Solution {
        List<List<String>> res = new ArrayList<>();
        LinkedList<String> temp = new LinkedList<>();

        public List<List<String>> partition(String s) {
            backtracking(s, 0);
            return res;
        }

        private void backtracking(String s, int start) {
            if (start >= s.length()) {
                res.add(new ArrayList(temp));
                return;
            }
			/**
             * 注意：因为只有回文字符串需要进行处理
             * 所以当判断不是回文字符串从而进行else语句时
             * 不需要进行任何处理，所以continue;跳出当前循环
             */
            for (int i = start; i < s.length(); i++) {
                if (isPalindrome(s, start, i)) {
                    String substring = s.substring(start, i + 1);
                    temp.add(substring);
                } else {
                    continue;
                }
                //为了保证不重复
                backtracking(s, i + 1);
                //回溯
                temp.removeLast();
            }
        }

        private boolean isPalindrome(String str, int left, int right) {
            for (int i = left, j = right; i < j; i++, j--) {
                if (str.charAt(i) != str.charAt(j)) {
                    return false;
                }
            }
            return true;
        }
    }

93. 复原 IP 地址

pointNum：记录逗点的数量

终止条件：当pointNum的值等于3时，说明字符串已被分成4段，此时只需要判断第四段字符串是否合法，如果合法，则说明该切割组合符合题目要求，加入到结果中即可

截取字符串：在for循环遍历字符串中for (int i = start; i < s.length(); i++)，[start, i]就是截取的子字符串，我们需要判断当前字符串是否合法，如果合法，就在截取的子字符串后面加上逗点，然后再进行递归回溯

注意：因为切割后的字符串后加上了逗点，所以下次递归的起始位置应该是当前位置+2

class Solution {
    List<String> res = new ArrayList<>();

    public List<String> restoreIpAddresses(String s) {
        backTracking(s,0,0);
        return res;
    }

    private void backTracking(String s, int start, int pointNum){
        //当添加的逗点为3时，分割结束
        if (pointNum == 3){
            //判断第四段字符串是否合法，如果合法就放进结果里
            if (isLegal(s,start,s.length()-1)){
                res.add(s);
            }
            return;
        }
        for (int i = start; i < s.length(); i++) {
            //判断[start,i]的字符串是否合法
            if (isLegal(s,start,i)){
                //在切割后的字符串后面加上逗点
                s = s.substring(0,i+1)+"."+s.substring(i+1);
                /**
                 * 递归+隐藏回溯
                 * 因为切割后的字符串后加上了逗点
                 * 所以下次递归的起始位置应该是当前位置+2
                 */
                backTracking(s, i+2, pointNum+1);
                //回溯，删除逗点
                s=s.substring(0,i+1)+s.substring(i+2);
            }else {
                break;
            }
        }
    }

    //判断字符串在[start,end]区间内是否合法
    private boolean isLegal(String s, int start, int end) {
        if (start > end) {
            return false;
        }
        //0开头不合法
        if (s.charAt(start) == '0' && start != end) {
            return false;
        }
        int num = 0;
        for (int i = start; i <= end; i++) {
            //非数字不合法
            if (s.charAt(i)>'9'||s.charAt(i)<'0'){
                return false;
            }
            //数字超过255不合法
            num = num*10+(s.charAt(i) - '0');
            if (num>255){
                return false;
            }
        }
        return true;
    }
}

子集问题

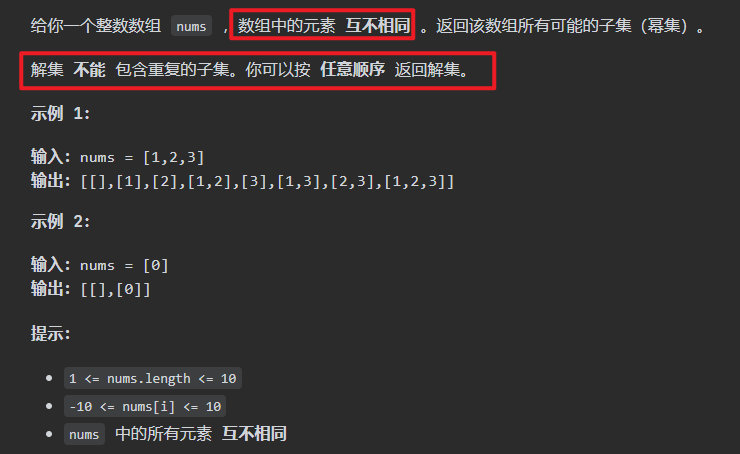
78. 子集

分割问题和组合问题都是收集树的叶子结点，而子集问题是找树的所有结点

因为要收集所有的结点，所以需要在递归函数的最开始对元素进行收集

注意：因为子集是无序的。{1, 2, 3}与{2, 3, 1}是一样的，所以取过的元素不会重复取

class Solution {
    List<List<Integer>> res = new ArrayList<>();
    LinkedList<Integer> temp = new LinkedList<>();

    public List<List<Integer>> subsets(int[] nums) {
        backTracking(nums,0);
        return res;
    }
    private void backTracking(int[] nums,int start){
        //遍历这个树的时候，记录所有节点
        res.add(new ArrayList<>(temp));
        //当满足该条件时，本层的for循环遍历也已经结束了，可以不加该条件
//        if (start >= nums.length){
//            return;
//        }
        for (int i = start; i < nums.length; i++) {
            temp.add(nums[i]);
            //不能取重复的元素，所以递归时应从下一位开始
            backTracking(nums,i+1);
            temp.removeLast();
        }
    }
}

90. 子集 II

该题与40. 组合总和 II类似，因为原数组包含重复元素，所以该题需要对结果进行去重（具体思路参考40. 组合总和 II）

先对原数组进行排序
去重针对同一树层的元素
去重不针对同一树枝的元素

使用used数组进行标记

class Solution {
    List<List<Integer>> res = new ArrayList<>();
    LinkedList<Integer> temp = new LinkedList<>();
    boolean[] used;

    public List<List<Integer>> subsetsWithDup(int[] nums) {
        used = new boolean[nums.length];
        Arrays.sort(nums);
        backTracking(nums, 0, used);
        return res;
    }

    private void backTracking(int[] nums, int start, boolean[] used) {
        res.add(new ArrayList<>(temp));
        if (start >= nums.length) {
            return;
        }
        for (int i = start; i < nums.length; i++) {
            //注意此处 !used[i - 1]
            if (i > 0 && nums[i] == nums[i - 1] && !used[i - 1]) {
                continue;
            }
            used[i] = true;
            temp.add(nums[i]);
            backTracking(nums, i + 1, used);
            temp.removeLast();
            used[i] = false;
        }
    }
}

不使用used数组进行标记

class Solution {
    List<List<Integer>> res = new ArrayList<>();
    LinkedList<Integer> temp = new LinkedList<>();

    public List<List<Integer>> subsetsWithDup(int[] nums) {
        Arrays.sort(nums);
        backTracking(nums, 0);
        return res;
    }

    private void backTracking(int[] nums, int start) {
        res.add(new ArrayList<>(temp));
        if (start >= nums.length) {
            return;
        }
        for (int i = start; i < nums.length; i++) {
            //注意此处的判断条件
            if (i > start && nums[i] == nums[i - 1]) {
                continue;
            }
            temp.add(nums[i]);
            backTracking(nums, i + 1);
            temp.removeLast();
        }
    }
}

排列问题

491. 递增子序列

终止条件：改题类似求子集问题，遍历树形结构找每一个节点，但是题目要求递增子序列大小至少为2，所以当临时数组temp.size()大于1的时，就可以将该组合进行收集

该题的重点是，在同一个数层中，如果出现了两个相同的元素，那么不能重复使用，不然会导致结果出现重复情况，所以可以通过一个map来进行去重，在遍历中先在map中进行判断，如果该元素在map中存在，则直接跳过，反之则对其进行标记

class Solution {
        List<List<Integer>> res = new ArrayList<>();
        LinkedList<Integer> temp = new LinkedList<>();
        public List<List<Integer>> findSubsequences(int[] nums) {
            backTracking(nums, 0);
            return res;
        }
        private void backTracking(int[] nums, int start) {
            // 当递增子序列中有两个元素时，就可以将该组合收集为结果
            if (temp.size() > 1) {
                res.add(new ArrayList<>(temp));
            }
            HashMap<Integer, Integer> map = new HashMap<>();
            for (int i = start; i < nums.length; i++) {
                // 进行剪枝操作
                if (!temp.isEmpty() && nums[i] < temp.getLast()) {
                    continue;
                }
                // 使用过了当前数字
                if (map.getOrDefault(nums[i], 0) >= 1) {
                    continue;
                }
                // 对使用过的元素进行标记
                map.put(nums[i], map.getOrDefault(nums[i], 0) + 1);
                temp.add(nums[i]);
                backTracking(nums, i + 1);
                temp.removeLast();
            }
        }
    }

棋盘问题

待补充

其他

待补充