理论基础
栈的特点:先进后出

栈提供了push和pop等接口,所有元素都必须符合先进后出的规则
可以理解为:栈是以底层容器完成其所有的工作,堆外提供统一的接口,我们可以选择用各种容器来实现栈的功能
java中栈的常见方法

队列的特点:先进后出
实际上是一种特殊的线性表,它只允许在表的前端进行删除操作,而在表的后端进行插入操作
java中队列的常见方法

定义两个栈,一个出栈(output),一个入栈(input),当元素进入队列时,先让元素全部进入名为input的栈,然后再让元素全部从input中pop出来,进入output栈,实现队列先进先出的特点

注意:当output栈为空时,就将input栈全部弹出并压入output栈中,然后output进行出栈操作。如果input栈没有全部弹出,就无法实现队列的特点
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
| class MyQueue {
private Stack<Integer> input;
private Stack<Integer> output;
public MyQueue() {
input = new Stack<>();
output = new Stack<>();
}
public void push(int x) {
input.push(x);
}
public int pop() {
if(output.isEmpty()){
while(!input.isEmpty()){
output.push(input.pop());
}
}
return output.pop();
}
public int peek() {
if(output.isEmpty()){
while(!input.isEmpty()){
output.push(input.pop());
}
}
return output.peek();
}
public boolean empty() {
return input.isEmpty() && output.isEmpty();
}
}
|
用队列实现栈
方法一:使用两个队列
创建两个队列que1和que2,先让元素全部进入que1,然后将除que1以外的所有元素全部备份到que2,然后将que1中剩下的那个元素弹出。最后再将que2中的元素,从que2中导回到que1,以此类推,直到最后一个元素从que1中弹出为止


代码如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
| class MyStack {
private Queue<Integer> que1;
private Queue<Integer> que2;
public MyStack() {
que1 = new LinkedList<>();
que2 = new LinkedList<>();
}
public void push(int x) {
que2.offer(x);
while (!que1.isEmpty()){
que2.offer(que1.poll());
}
Queue<Integer> temp;
temp = que1;
que1 = que2;
que2 = temp;
}
public int pop() { return que1.poll(); }
public int top() { return que1.peek(); }
public boolean empty() { return que1.isEmpty(); }
}
|
方法二:使用一个队列
Java双端队列Deque使用详解
创建队列que,假如弹出的元素顺序是3 <= 2 <= 1,此时队列中元素的顺序为3 <= 2 <= 1,那么就需要将队列中的前两个元素先弹出去,再重新加入队列。经过上面的操作后,队列中元素的顺序为1 <= 3 <= 2,此时就把1弹出去,作为结果。然后继续将3弹出去,再重新加入队列,此时元素顺序为2 <= 3,此时,再将2与3弹出,作为结果,即为答案
总结:将队列中的size-1个元素弹出后,再次加入队列,第size个元素弹出作为结果,以此类推,直到最后两个元素时,直接将它们弹出即为答案
代码实现:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
| class MyStack {
private Deque<Integer> queue;
public MyStack() {
queue = new LinkedList<>();
}
public void push(int x) { queue.addLast(x); }
public int pop() {
int size = queue.size()-1;
while (size > 0){
queue.addLast(queue.peekFirst());
queue.pollFirst();
--size;
}
return queue.pollFirst();
}
public int top() { return queue.peekLast(); }
public boolean empty() { return queue.isEmpty(); }
}
|

情况一:字符串里左方向的括号多余了 ,所以不匹配
解决:当遍历完字符串,发现栈不为空,说明有多余的字符串

情况二:括号没有多余,但是 括号的类型没有匹配上
解决:在遍历字符串匹配的过程中,发现栈里没有要匹配的字符,说明有不匹配的字符串

情况三:字符串里右方向的括号多余了,所以不匹配
解决:在遍历字符串匹配的过程中,栈已经为空了,没有匹配的字符了,说明右括号没有找到对应的左括号
注意:在匹配左括号的时候,右括号先入栈,就只需要比较当前元素和栈顶相不相等就可以
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
| class Solution {
public boolean isValid(String s) {
if (s.length() == 0){
return true;
}
if (s.length() % 2 != 0){
return false;
}
Stack<Character> stack = new Stack<>();
for (char ch : s.toCharArray()) {
if (ch == '(' || ch == '{' || ch =='['){
stack.push(ch);
}else {
if (stack.isEmpty()){
return false;
}
char temp = stack.pop();
if (ch == ')'){
if (temp != '('){
return false;
}
}
if (ch == '}'){
if (temp != '{'){
return false;
}
}
if (ch == ']'){
if (temp != '['){
return false;
}
}
}
}
return stack.isEmpty();
}
}
|
方法二:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
| class Solution {
public boolean isValid(String s) {
if(s.isEmpty())
return true;
Stack<Character> stack=new Stack<Character>();
for(char c:s.toCharArray()){
if(c=='(')
stack.push(')');
else if(c=='{')
stack.push('}');
else if(c=='[')
stack.push(']');
else if(stack.empty()||c!=stack.pop())
return false;
}
if(stack.empty())
return true;
return false;
}
}
|

思路:先将字符串转换为字符数组,并取出每个字符。当栈中没有元素的时候,就将字符push进栈。
当栈中已经存在元素时,先比较当前字符和栈中的第一个元素是否相同,如果相同,则将栈中元素弹出,如果不相同,则将元素进行push进栈。直到最后每个字符都遍历完,栈中所存放的元素即为目标值
方法一:使用栈
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
| public String removeDuplicates(String s) {
Stack<Character> stack = new Stack();
for (char ch : s.toCharArray()) {
if (stack.isEmpty() || stack.peek() != ch){
stack.push(ch);
}else {
stack.pop();
}
}
String res = "";
while (!stack.isEmpty()){
res = stack.pop() + res;
}
return res;
}
|
方法二:使用StringBuffer模拟栈实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
| public String removeDuplicates(String s) {
StringBuffer res = new StringBuffer();
int top = -1;
for (int i = 0; i < s.length(); i++) {
char ch = s.charAt(i);
if (top >= 0 && res.charAt(top) == ch){
res.deleteCharAt(top);
top--;
}else {
res.append(ch);
top++;
}
}
return res.toString();
}
|


思路:遇到符号则把栈中两个元素弹出,在进行计算后,将结果push到栈中,在遇到数字时,则直接将其push进栈
注意:注意减号和除号在计算中,要将后弹出的元素作为 被减数/被除数
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
| public int evalRPN(String[] tokens) {
Stack<Integer> stack = new Stack<>();
for (String str : tokens) {
if (str.equals("+")){
Integer num1 = stack.pop();
Integer num2 = stack.pop();
stack.push(num1+num2);
} else if (str.equals("-")){
Integer num1 = stack.pop();
Integer num2 = stack.pop();
stack.push(num2-num1);
} else if (str.equals("*")){
Integer num1 = stack.pop();
Integer num2 = stack.pop();
stack.push(num1*num2);
} else if (str.equals("/")){
Integer num1 = stack.pop();
Integer num2 = stack.pop();
stack.push(num2/num1);
}else {
stack.push(Integer.valueOf(str));
}
}
return stack.pop();
}
|
思路:维护一个单调的优先队列,保证队列入口是为当前滑动窗口的最大值
当滑动窗口进行移动时,先判断要移除的元素是否与当前队列入口处的元素相同,如果相同则说明该元素已经不在当前滑动窗口内,则将该元素pop出去。如果不相同,则不进行任何操作。
在进行上一步的判断后,需要将滑动窗口新添加的元素,push进队列,如果加入进来的元素大于它之前的元素,则直接将它之前的元素全部pop出去,不进行维护

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
| class MyQueue{
Deque<Integer> deque = new ArrayDeque();
public void add(int val) {
while (!deque.isEmpty() && deque.getLast() < val){
deque.removeLast();
}
deque.addLast(val);
}
public int peek() {
return deque.peek();
}
public void poll(int val) {
if (!deque.isEmpty() && deque.peek() == val){
deque.poll();
}
}
}
class Solution {
public int[] maxSlidingWindow(int[] nums, int k) {
if (nums.length == 1) {
return nums;
}
int len = nums.length - k + 1;
int[] res = new int[len];
int num = 0;
MyQueue myQueue = new MyQueue();
for (int i = 0; i < k; i++) {
myQueue.add(nums[i]);
}
res[num++] = myQueue.peek();
for (int i = k; i < nums.length; i++) {
myQueue.poll(nums[i - k]);
myQueue.add(nums[i]);
res[num++] = myQueue.peek();
}
return res;
}
}
|
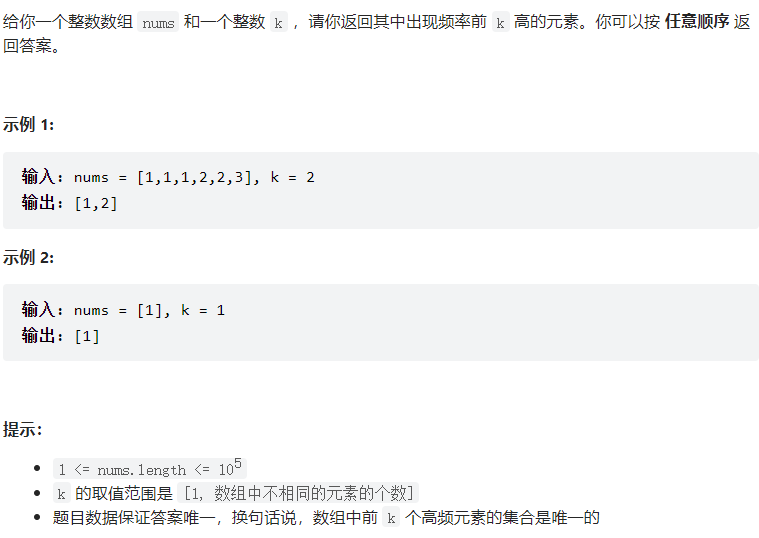
单调栈专题(待补充)