哈希表
概念
哈希表是根据关键码的值而直接进行访问的数据结构。实际上其实数组也是一张哈希表,哈希表中关键码就是数组的索引下标,然后通过下标直接访问数组中的元素
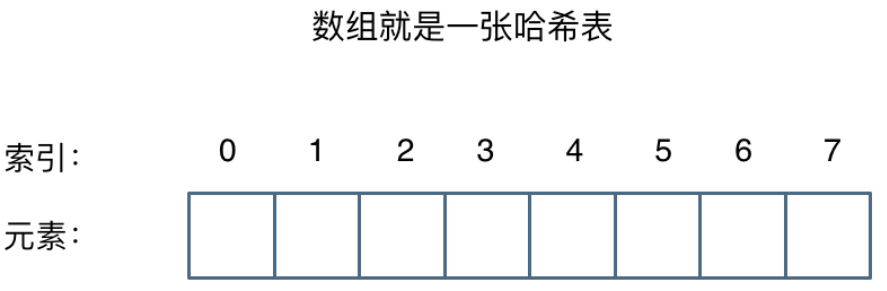
一般哈希表都是用来快速判断一个元素是否出现集合里
哈希法是牺牲了空间换取了时间,因为要使用额外的数组,set或者是map来存放数据,才能实现快速的查找
哈希函数
哈希函数,就是将元素直接映射为哈希表上的索引,然后就可以通过查询索引下标进行快速访问
哈希函数如下图所示,通过hashCode把名字转化为数值,一般hashcode是通过特定编码方式,可以将其他数据格式转化为不同的数值。
拉链法
当出现哈希碰撞的时候,发生冲突的元素都被存储在链表中
拉链法就是要选择适当的哈希表的大小,这样既不会因为数组空值而浪费大量内存,也不会因为链表太长而在查找上浪费太多时间。
线性探测法
使用线性探测法,一定要保证哈希表大小大于数据大小。 因为需要依靠哈希表中的空位来解决碰撞问题
如果出现冲突的位置,那么就向下找一个空位放置。所以要求tableSize一定要大于dataSize ,要不然哈希表上就没有空置的位置来存放冲突的数据了
结合数组

定义一个数组记录字符串s里字符出现的次数。然后将把字符映射到数组也就是哈希表的索引下标上,因为字符a到字符z的ASCII是26个连续的数值,所以字符a映射为下标0,相应的字符z映射为下标25
首先遍历字符串s,将 s[i] - 'a' 所在的元素做++ ,这样就将字符串s中字符出现的次数,统计出来了
然后再遍历字串t,对t中出现的字符映射数组索引上的数值再做–
最后,检查数组上有无元素不为零,如果又,就说明s和t中字符出现的次数肯定不一样
时间复杂度为O(n),空间上因为定义了常量大小的辅助数组,空间复杂度为O(1)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
| public boolean isAnagram(String s, String t) {
int[] nums = new int[26];
for (char c : s.toCharArray()) {
nums[c-'a']++;
}
for (char c : t.toCharArray()) {
nums[c-'a']--;
}
for (int num : nums) {
if (num != 0) {
return false;
}
}
return true;
}
|
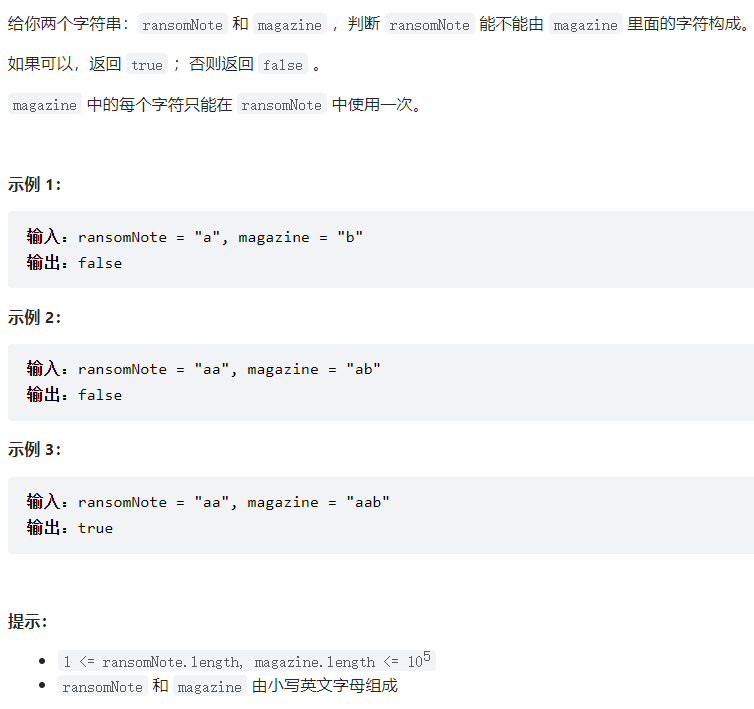
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
| public boolean canConstruct(String ransomNote, String magazine) {
int[] nums = new int[26];
for (char c : magazine.toCharArray()) {
nums[c - 'a']++;
}
for (char c : ransomNote.toCharArray()) {
nums[c - 'a']--;
}
for (int num : nums) {
if (num < 0){
return false;
}
}
return true;
}
|
结合Map

思路:
1、将不同的字符串转换为字符数组后进行排序
2、如果排序后结果相同,说明字母异位词相同
3、可以将排序后的结果作为map的key来进行存储,然后将字母异位词作为map的value进行存储
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
| public List<List<String>> groupAnagrams(String[] strs) {
Map<String, List<String>> map = new HashMap<>();
for (String str : strs) {
char[] array = str.toCharArray();
Arrays.sort(array);
String key = new String(array);
List<String> list = map.getOrDefault(key, new ArrayList<>());
list.add(str);
map.put(key,list);
}
return new ArrayList<List<String>>(map.values());
}
|

1、map用来存放我们访问过的元素,在遍历数组的时候,需要记录之前遍历过哪些元素和对应的下标,这样才能找到与当前元素相匹配的(也就是相加等于target)
2、map中的存储结构为 {key:数据元素,value:数组元素对应的下表}
3、在遍历数组的时候,只需要向map去查询是否有和目前遍历元素比配的数值,如果有,就找到的匹配对,如果没有,就把目前遍历的元素放进map中
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
| public int[] twoSum(int[] nums, int target) {
int[] res = new int[2];
if (nums == null || nums.length == 0) {
return res;
}
HashMap<Integer, Integer> map = new HashMap<>();
for (int i = 0; i < nums.length; i++) {
if (map.get(target - nums[i]) == null){
map.put(nums[i],i);
}else {
res[1] = i;
res[0] = map.get(target - nums[i]);
}
}
return res;
}
|

目标:找到A[i] + B[j] + C[k] + D[l] = 0即可
将数组1和数组2每一个相加后的值作为map集合的key,相加的值的个数作为map集合的value,如果该值出现多次,则让value继续++
遍历数组3和数组4,找到如果 0-(c+d) 在map中出现过的话,就用count把map中key对应的value也就是出现次数统计出来。count即为目标值
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
| public int fourSumCount(int[] nums1, int[] nums2, int[] nums3, int[] nums4) {
HashMap<Integer, Integer> map = new HashMap<>();
int res = 0;
for (int num1 : nums1) {
for (int num2 : nums2) {
int temp = num1 + num2;
if (map.containsKey(temp)) {
map.put(temp,map.get(temp)+1);
}else {
map.put(temp,1);
}
}
}
for (int num3 : nums3) {
for (int num4 : nums4) {
int temp = num3 + num4;
if (map.containsKey(0-temp)) {
res += map.get(0-temp);
}
}
}
return res;
}
|
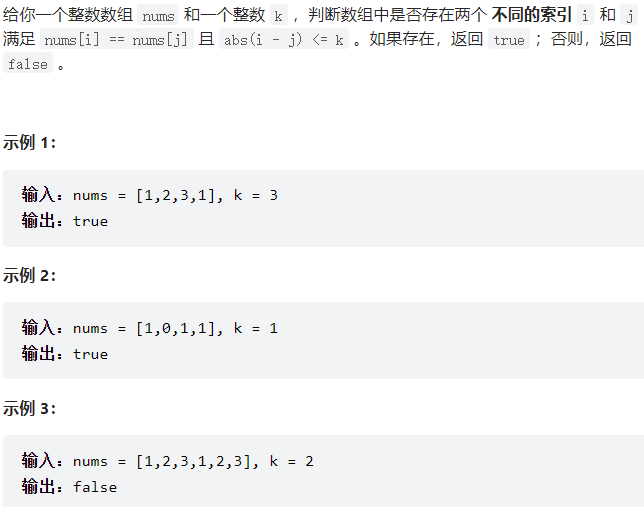
1
2
3
4
5
6
7
8
9
10
11
12
13
14
| class Solution {
public boolean containsNearbyDuplicate(int[] nums, int k) {
Map<Integer, Integer> map = new HashMap<>();
for (int i = 0; i < nums.length; i++) {
if (map.containsKey(nums[i])) {
if (Math.abs(i - map.get(nums[i])) <= k) {
return true;
}
}
map.put(nums[i],i);
}
return false;
}
}
|


1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
| public boolean wordPattern(String pattern, String s) {
HashMap<Character, String> map = new HashMap<>();
String[] strs = s.trim().split(" ");
if (pattern.length() != strs.length){
return false;
}
for (int i = 0; i < pattern.length(); i++) {
if (!map.containsKey(pattern.charAt(i))) {
if (map.containsValue(strs[i])) {
return false;
}
map.put(pattern.charAt(i),strs[i]);
}else {
if (!map.get(pattern.charAt(i)).equals(strs[i])) {
return false;
}
}
}
return true;
}
|

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
| public boolean isIsomorphic(String s, String t) {
return isIsomorphicTwo(s, t) && isIsomorphicTwo(t, s);
}
public boolean isIsomorphicTwo(String s, String t) {
int n = s.length();
HashMap<Character, Character> map = new HashMap<>();
for (int i = 0; i < n; i++) {
char c1 = s.charAt(i);
char c2 = t.charAt(i);
if (map.containsKey(c1)) {
if (map.get(c1) != c2) {
return false;
}
} else {
map.put(c1, c2);
}
}
return true;
}
|
结合Set

解法一:使用set
1、先判断nums1和nums2有没有一个为空,有则说明无交集
2、创建两个HashSet,先把nums1中的所有数据加入到set1中,然后遍历nums2,如果set1中出现了与nums2中数据相同的,说明该数为交集,则加入到set2中
3、创建目标数组,将set2的数据放到目标数组并返回
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
| public int[] intersection(int[] nums1, int[] nums2) {
if (nums1 == null || nums1.length == 0 || nums2 == null || nums2.length == 0) {
return new int[0];
}
HashSet<Integer> set1 = new HashSet<>();
HashSet<Integer> set2 = new HashSet<>();
for (int num1 : nums1) {
set1.add(num1);
}
for (int num2 : nums2) {
if (set1.contains(num2)) {
set2.add(num2);
}
}
int[] target = new int[set2.size()];
int left = 0;
for (int num2 : set2) {
target[left++] = num2;
}
return target;
}
|
解法二:使用哈希表
1、创建一个临时数组,并用nums1每个元素的值num1作为临时数组索引,并让索引处的元素加一
注意:此处要判断元素是否为0,为了防止出现重复元素而++两次
2、将nums2每个元素的值num2作为临时数组索引,判断索引处对应的元素是否为0,如果不是则说明该数即为交集,添加到list中。
注意:此处需要将临时数组对应索引的元素置空,为了防止出现重复元素导致list集合出现重复元素
3、将list中的数据遍历到目标数组并返回
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
| public int[] intersection(int[] nums1, int[] nums2) {
if (nums1 == null || nums2 == null || nums1.length == 0 || nums2.length == 0){
return new int[0];
}
int[] temp = new int[1001];
List<Integer> list = new ArrayList<>();
for(int i = 0;i < nums1.length ;i++){
if(temp[nums1[i]] == 0){
temp[nums1[i]]++;
}
}
for(int i = 0;i < nums2.length ;i++){
if(temp[nums2[i]] == 1){
list.add(nums2[i]);
temp[nums2[i]] = 0;
}
}
int[] target = new int[list.size()];
for(int i = 0;i < list.size() ;i++){
target[i] = list.get(i);
}
return target;
}
|

解法一:快慢指针思想
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
| public boolean isHappy(int n) {
int slow = create(n);
int fast = create(create(n));
while (slow != fast) {
slow = create(slow);
fast = create(create(fast));
}
return slow == 1 ? true : false;
}
private int create(int n) {
int sum = 0;
while (n > 0) {
sum += (n % 10) * (n % 10);
n /= 10;
}
return sum;
}
|
解法二:哈希集合检测
1、创建一个hashset,将数字添加进set集合中
2、添加时判断集合中是否有这个元素,并且该数字不为1,如果以上条件都满足,则说明还没有进行循环
3、如果以上条件不满足,说明已经进入了循环,此时判断该数是否为1,如果是则为快乐数
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
| public boolean isHappy(int n) {
Set<Integer> set = new HashSet<>();
while (n != 1 && !set.contains(n)) {
set.add(n);
n = getNum(n);
}
return n == 1;
}
private int getNum(int n) {
int sum = 0;
while (n > 0) {
sum += (n % 10) * (n % 10);
n /= 10;
}
return sum;
}
|
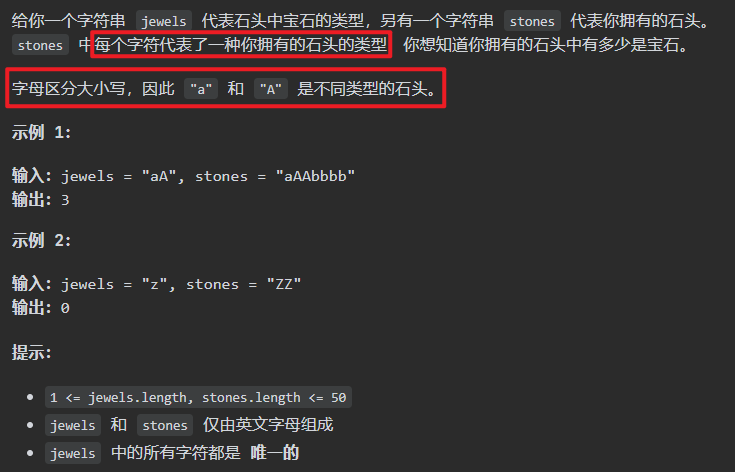
首先对字符串jewels进行遍历,将字符分别存到HashSet中,以便之后遍历stones的时候进行查找
遍历stones,并将每个字符与HashSet中的进行比对,如果字符存在,则说明存在一个宝石,让结果count++,遍历结束,返回count即为答案
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
| class Solution {
public int numJewelsInStones(String jewels, String stones) {
int count = 0;
HashSet<Character> set = new HashSet<>();
for (int i = 0; i < jewels.length(); i++) {
char jewel = jewels.charAt(i);
set.add(jewel);
}
for (int i = 0; i < stones.length(); i++) {
char stone = stones.charAt(i);
if (set.contains(stone)) {
count++;
}
}
return count;
}
}
|
其他

解法一:哈希映射
……待补充

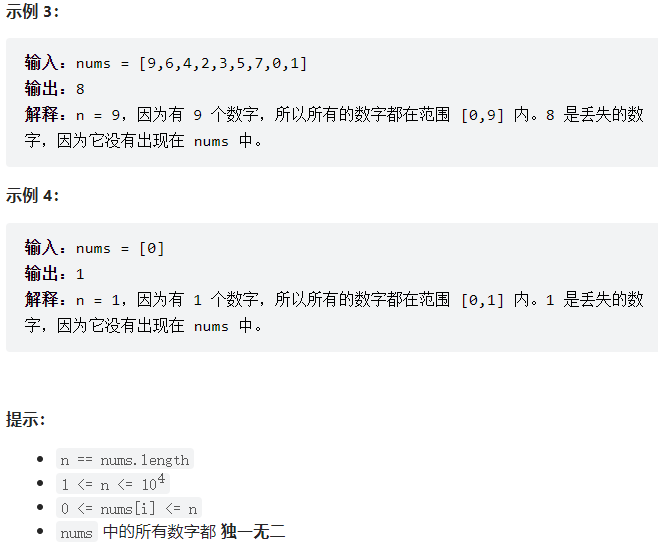
方法一:哈希表
1
2
3
4
5
6
7
8
9
10
11
12
13
| public int missingNumber(int[] nums) {
HashMap<Integer, Integer> map = new HashMap<>();
int res = 0;
for (int i = 0; i < nums.length; i++) {
map.put(nums[i],i);
}
for (int i = 0; i <= nums.length; i++) {
if (!map.containsKey(i)){
res = i;
}
}
return res;
}
|
方法二:排序
1
2
3
4
5
6
7
8
9
| public int missingNumber(int[] nums) {
Arrays.sort(nums);
for (int i = 0; i < nums.length; i++) {
if (nums[i] != i) {
return i;
}
}
return nums.length;
}
|



















